Problem in Which a Avl Tree Should Be Used
First add a number 90. What youre proposing using an AVL tree per bucket does make the worst-case performance of a lookup asymptotically better but for it to be worthwhile you need to have a lot of collisions.
Implement an AVL Tree.

. AVL tree may become unbalanced if a node is inserted in the left subtree of the left subtree. And 30 and 70 are the level 1. Complete this file by implementing the insert and remove functions for AVL Trees.
And if the insertions and deletions are less frequent and search is the more frequent operation then AVL tree should be preferred over Red Black Tree. Another variation of balanced trees is red-black trees. Following is the post for delete.
Median in a stream of integers running integers. Your tree should be a Binary Search tree that is self-balancing. Thus in some cases searching insertion and removal is no better than in a sequence.
If a word appears on the same line twice it. If a word already exists in the AVL Tree simply add the new line number to the existing node. The means that each node has its hash computed and is stored inside it and the hash of the node depends on the hashes of both child nodes.
Insert - Takes an item of the templated type and inserts it into the AVL tree re-balancing if necessary according to the AVL Tree. Complete this file by implementing the insert and erase ie. 50 30 70 To the sample AVL tree you will add two numbers.
AVL Tree Implementation. Since all new keys are inserted. When presented with the task of writing an AVL tree class in Java I was left scouring the web for useful information on how this all works.
AVL Trees 38 Arguments for AVL trees. However in the worst-case search insertion and removal time is On if the height of the tree is equal to n. Label each node in the resulting tree with its balance factor.
AVL Tree Implementation Problem Solving with Algorithms and Data Structures. AVL trees by definition are required to meet the balance condition after every operation. This creates a slight overhead in the insertion and deletion of elements if you keep track of the heights of subtrees in each node the timing difference is minimal but allows for more efficient searches.
If there are n nodes in AVL Tree its maximum height can not exceed 144log 2 n. It essentially is an AVL tree which is in turn a balanced binary tree which stores its keys and values in leaf nodes and only technical data in branches. The height balancing adds no more than a constant factor to the speed of insertion.
Searching in the tree is straight forward but when we add an element to the tree we might have to re-arrange the nodes to preserve the AVL property. It should use the AVL algorithm as discussed in class and should be implemented as a template class with the following public methods. AVL Trees 11 Time Complexity Searching insertion and removal in a binary search tree is Oh where h is the height of the tree.
After that add a number 100. Difficult to program. Now that we have demonstrated that keeping an AVL tree in balance is going to be a big performance improvement let us look at how we will augment the procedure to insert a new key into the tree.
In AVL Tree we use balance factor for every node and a tree is said to be balanced if the balance factor of every node is 1 0 or -1. Problem 4 - AVL Trees 45 We are providing you a half-finished file avlbsth in the homework-resources repository for implementing an AVL Tree. For the AVL tree problems in the quiz use the level-by-level order to represent them.
In other words Worst case height of AVL Tree with n nodes 144log 2 n. Every time you insert or remove a key every node in the tree should have the AVL property. For example typically AVLs have faster lookup times than red-black trees but lower insertion and deletion times.
Replace a node with both children using an. To meet that requirement we need to restructure the tree periodically essentially detecting and correcting imbalance whenever and wherever it happens. To understand them better we should take.
An AVL A delson- V elski L andis tree is a binary search tree which maintains the following height-balanced AVL property at each node in the tree. Abs height of left subtree height of right subtree 1. AVL Trees 10 Points Given the following AVL Tree.
Create a function findOptimalSequence which takes two inputs - sorted array of integers and size of the array and returns the optimal sequence for AVL tree insertion. The AVL Tree Rotations Tutorial By John Hargrove Version 101 Updated Mar-22-2007 Abstract I wrote this document in an effort to cover what I consider to be a dark area of the AVL Tree concept. Double rotations are slightly complex version of already explained versions of rotations.
PRACTICE PROBLEMS BASED ON AVL TREE PROPERTIES- Problem-01. Search is Olog N since AVL trees are always balanced. More space for balance factor.
For the resulting AVL tree after two additions. Write the method public void indexWordString word int line that adds an occurrence of the word word in line line. An AVL tree is a fairly well balanced sorted binary tree where the depth of two branches will differ by at most one.
Usually each of them has some advantages faster operations and disadvantages slower operations. An AVL tree eliminates that problem by balancing itself. AVL Tree Set 2 Deletion Following are some posts that have used self-balancing search trees.
A Draw the resulting BST after 5 is removed but before any rebalancing takes place. Find the minimum number of nodes required to construct AVL Tree of height 3. For a sample tree below the root value 50 is the level O.
Problem 4 AVL Trees 40 We are providing you a half-finished file avlbsth in the homework-resources repository for implementing an AVL Tree. AVL tree is a self-balanced binary search tree. Theres a nifty result that says that if you have a sufficiently good hash function and drop n objects into an n-slot hash table the largest bucket has expected size Olog n log log.
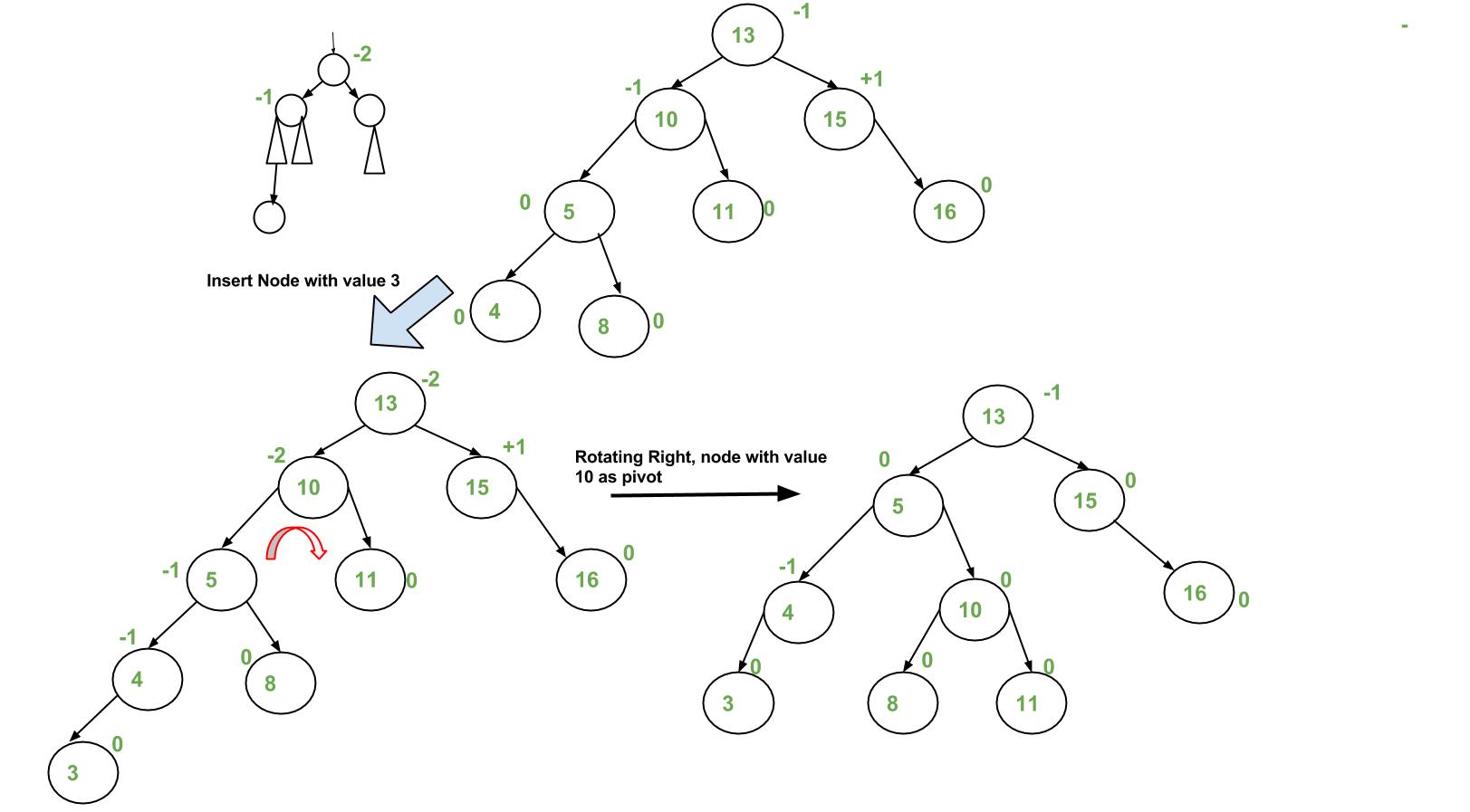
It builds on the file you completed for the previous question. As depicted the unbalanced node becomes the right child of its left child by performing a right rotation. The balance factor is the difference between the heights of left subtree and right subtree.
Insertion and deletions are also Ologn 3. Namely the left and right subtrees are of equal height or their heights differ by 1. By induction this means that any change.
Arguments against using AVL trees. Remove but we use erase to match stdmap functions for AVL Trees. You are strongly encouraged to use privateprotected helper functions.
Thus if the majority of your queries are lookups you should favor using AVL trees Continue Reading. The tree then needs a right rotation. Inside this function call a function to create an AVL tree from the sorted array and then call a function to find its level order traversal.
You are strongly encouraged to use. It builds on the file you completed for the previous question.
Data Structures Tutorials Avl Tree Examples Balance Factor

Avl Trees An Avl Tree Is A Self Balancing Binary By Randerson112358 Medium
Avl Tree A Tree That Can Stay Balanced By Rotating

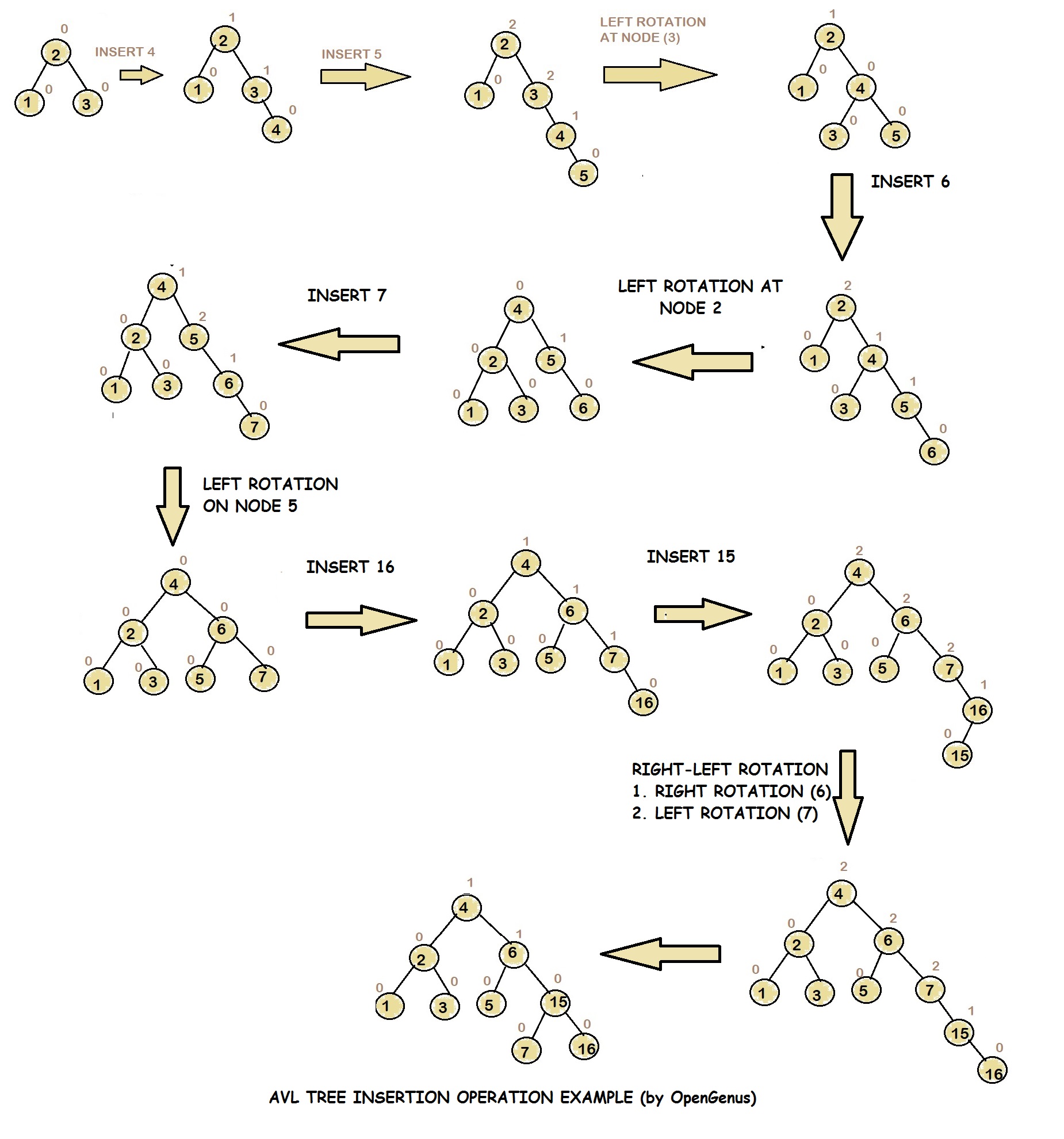
Avl Tree Set 1 Insertion Geeksforgeeks
Avl Tree Set 1 Insertion Geeksforgeeks

3 Example Of An Insert Operation That Violates The Avl Tree Balance Download Scientific Diagram
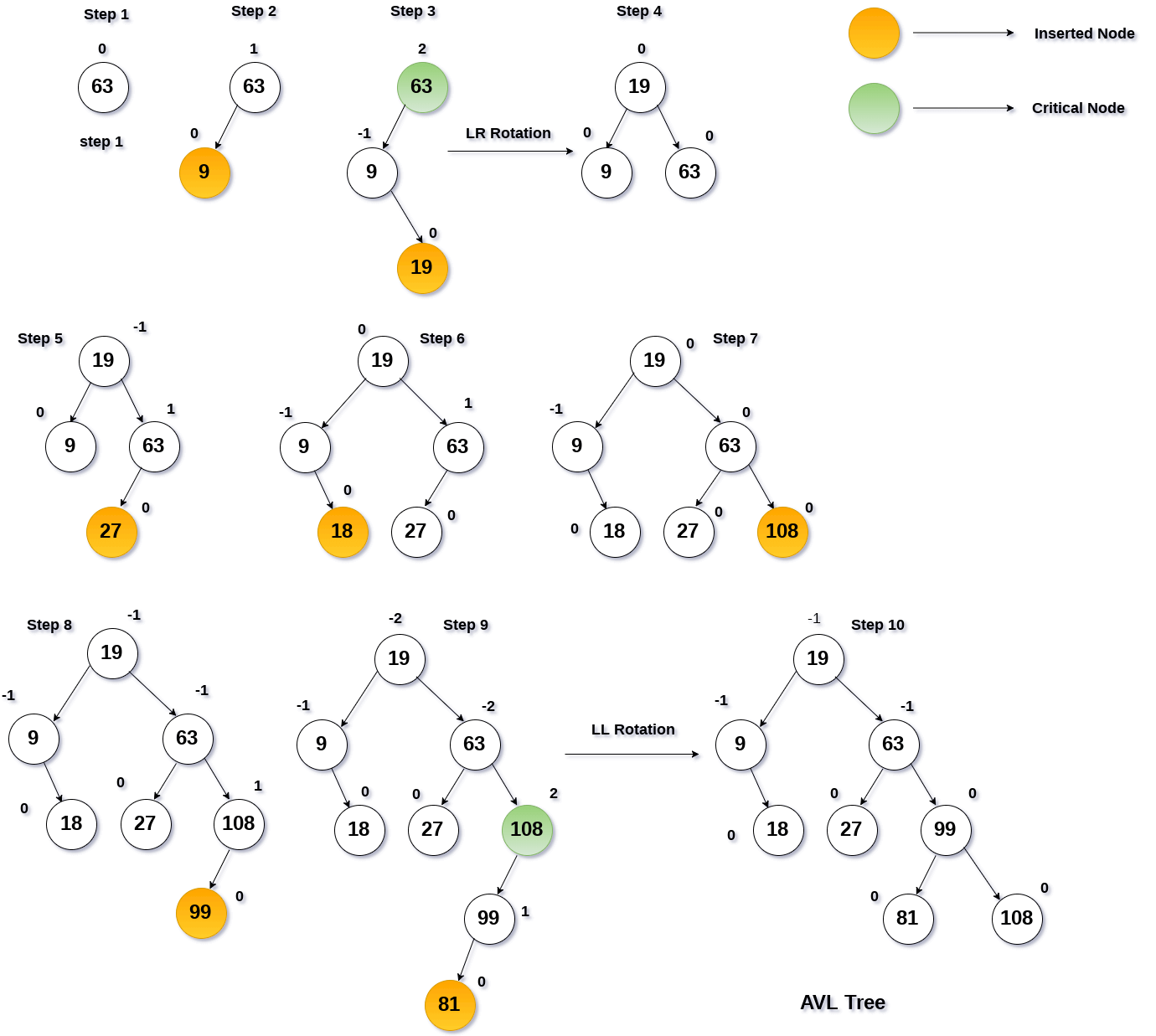
Insertion In Avl Tree Javatpoint
Avl Tree Set 1 Insertion Geeksforgeeks
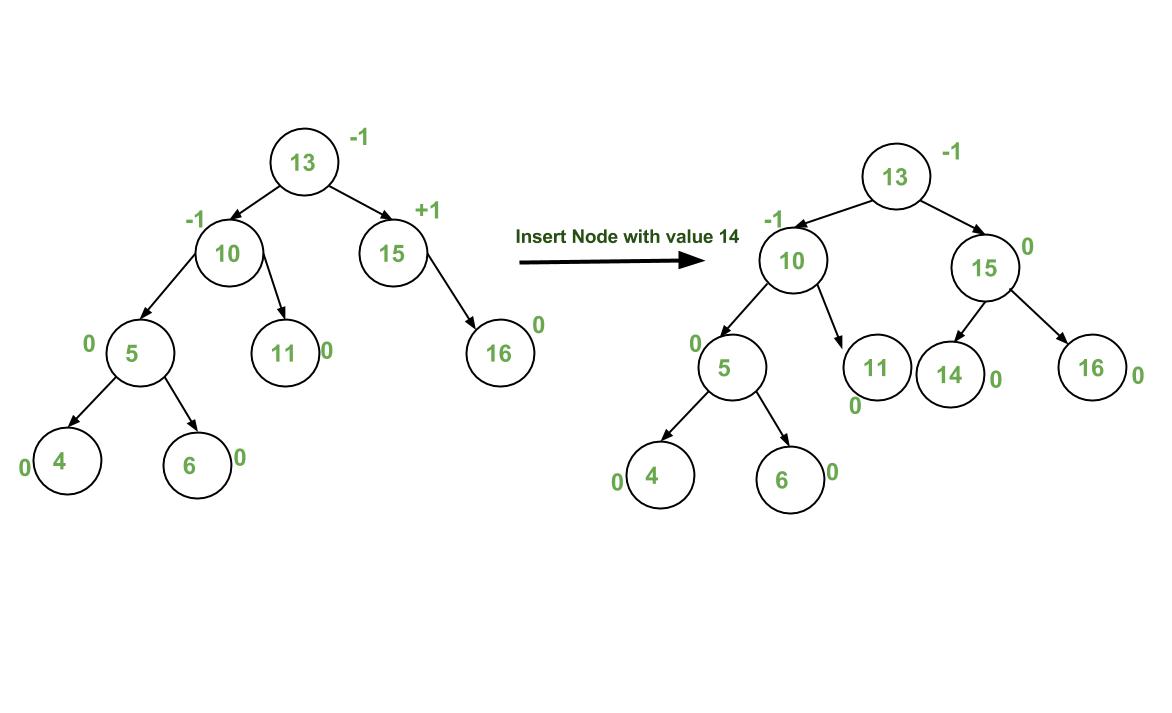
Avl Tree Set 1 Insertion Geeksforgeeks

Avl Tree And Heap Data Structure In C

Avl Trees Insertion Deletion And Analysis

Avl Tree Rotations Ll Rr Lr Rl With More Than 3 Nodes With Diagram Example Dsa Youtube
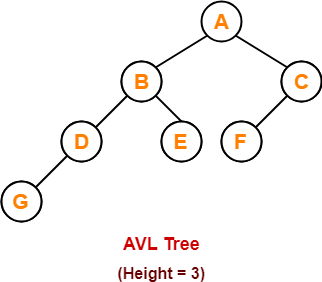
Avl Tree Properties Problems On Avl Tree Gate Vidyalay
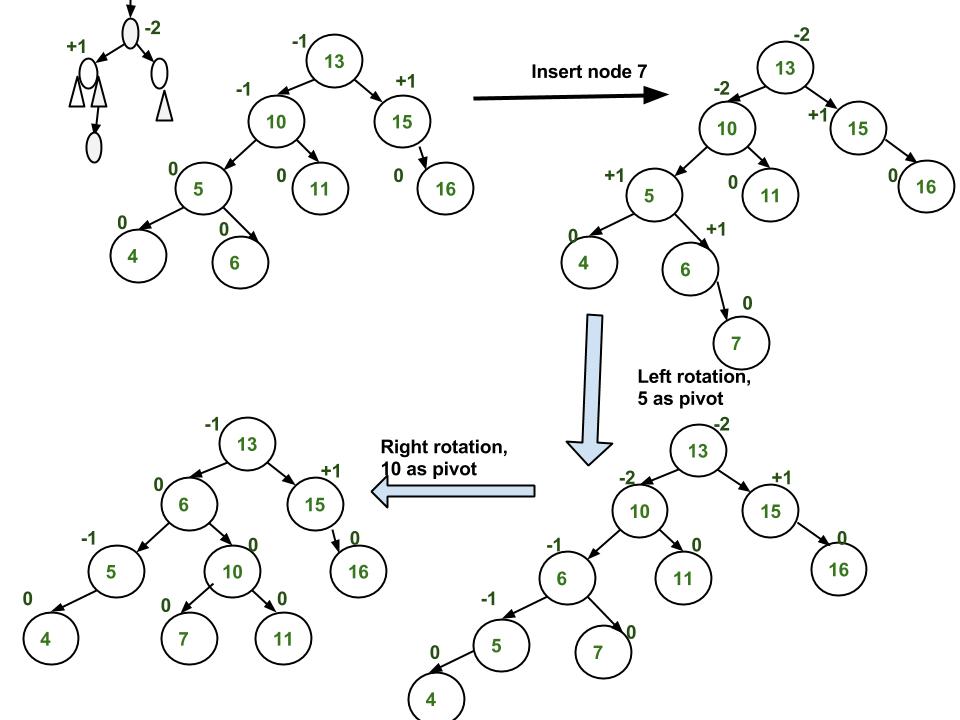
Avl Tree Set 1 Insertion Geeksforgeeks
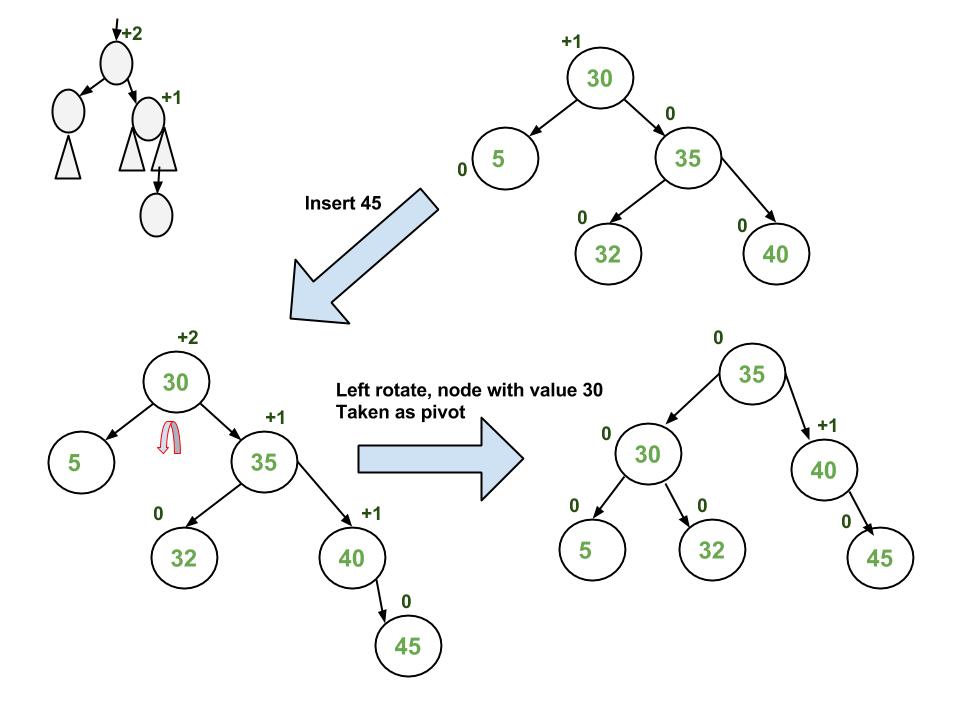
Avl Tree Set 1 Insertion Geeksforgeeks
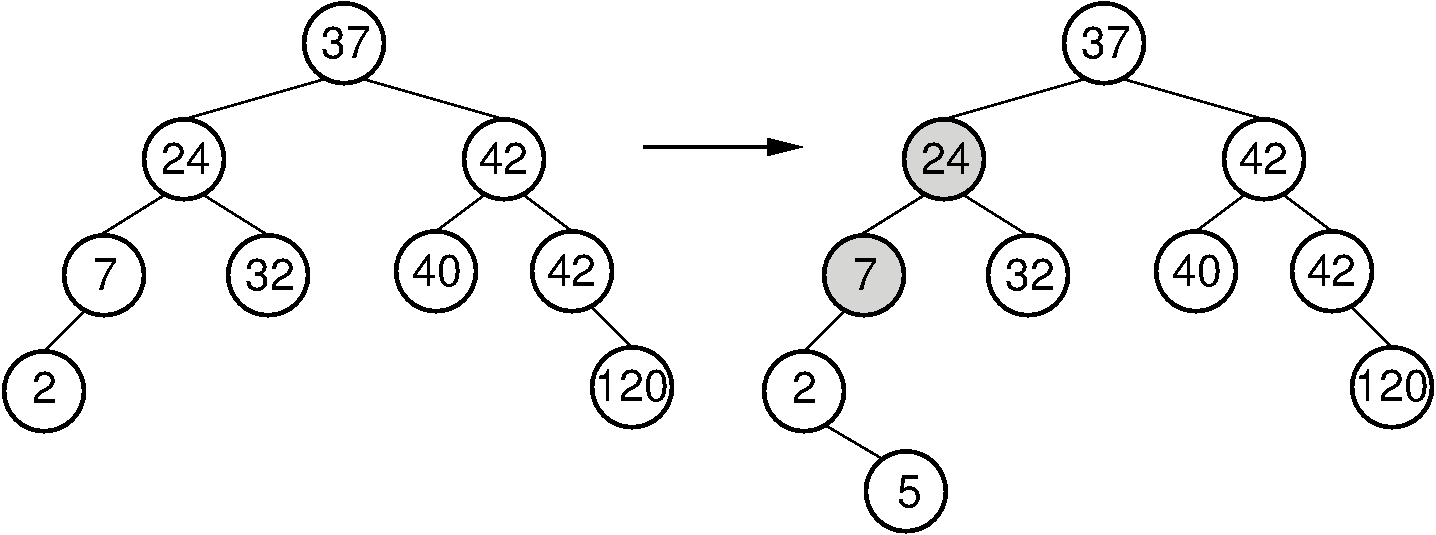
26 2 The Avl Tree Opendsa Data Structures And Algorithms Modules Collection


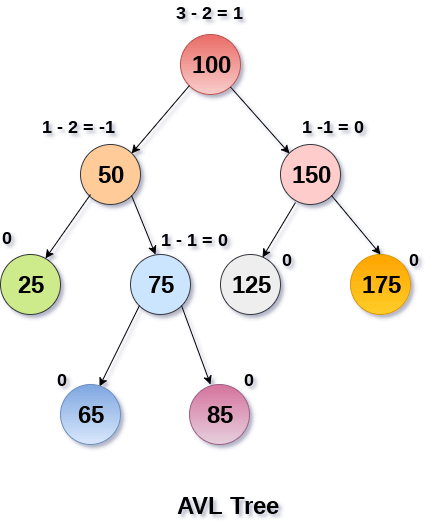


Comments
Post a Comment